In his book, The Wisdom of Crowds, James Surowiecki recounts how Francis Galton, a prominent statistician from the 19th century, attended an event at a country fair in England where the object was to guess the weight of an ox.
Individual contestants were relatively well informed on the subject (the audience was farmers), but their estimates were still quite variable. Nonetheless, the mean of all the estimates was surprisingly accurate – within 1% of the true weight of the ox (over half a ton). On balance the errors from multiple guesses tended to cancel one another out. The crowd’s average was more accurate than nearly all the individual estimates, hence the name of Surowiecki’s book. Diversity of estimates was a strength, not a drawback.
The analog in predictive modeling is ensemble learning. You can think of individual model predictions as estimates, akin to the farmers’ guesses as to the ox’s weight. In ensemble learning, predictions from multiple models (base learners) are averaged or voted, to yield improved predictive performance.
One Goal, Many Paths
(The following draws on a blog originally published by Jordan Barr in the January 17, 2020 Elder Research blog; I thank Jordan for permission to use it here)
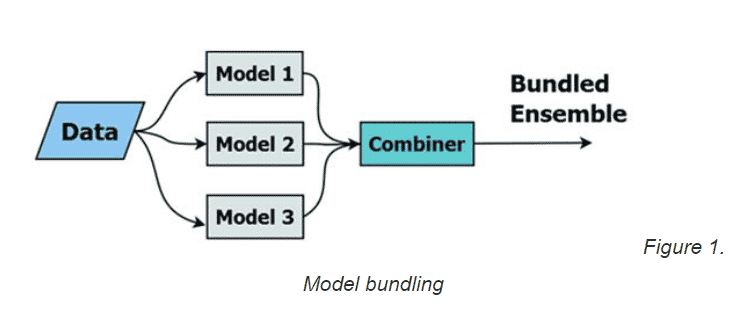
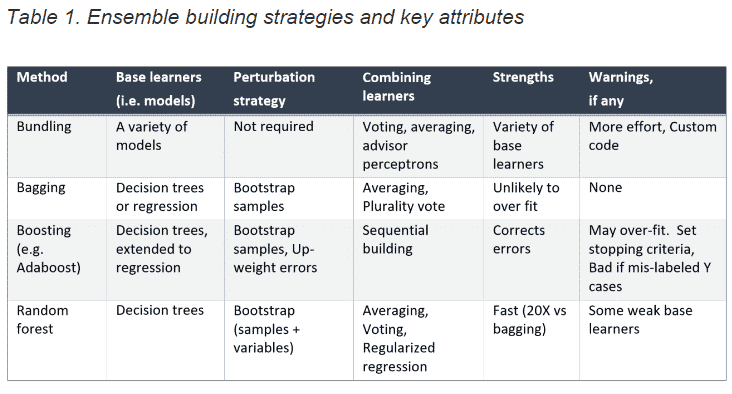
In the 1990s, Dr. John Elder, the Founder of Elder Research (which owns Statistics.com), discovered the marvel of ensembles while working on the challenge of predicting species of bats. He got different results among various base learners by using different types of modeling algorithms, and called the combination “model fusion” or “bundling.” His ensemble approach worked best when the base learners — such as decision trees, linear discriminate analysis (LDA), and neural networks (models 1, 2, and 3 in Figure 1) — each had some predictive power on its own. He found that if a method was prone to overfitting (e.g. trees and neural nets), the ensembling could compensate.
Figure 1. Model bundling
Usually, bundling a subset of relatively “good” base learners resulted in better overall performance, but sometimes combinations behaved in surprising ways. In general, the more learners combined, the better the expected performance. And, to date, ensembles of trees have always outperformed individual trees out-of-sample. (Ensemble Methods in Data Mining: Seni & Elder (2010) www.tinyurl.com/book2ERI )
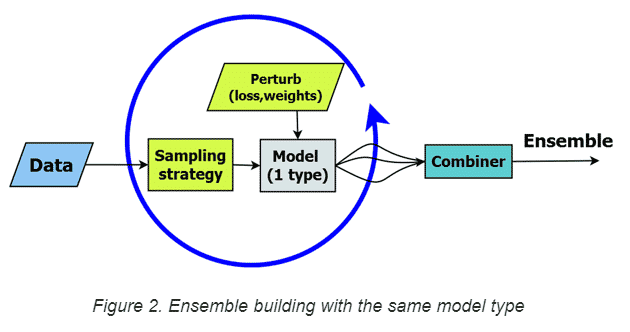
Others discovered that another way to create diversity in the base learners is to vary the cases (rather than the model type) through bootstrap aggregation (aka bagging). Each model is trained using a different random sample (see “sampling strategy” in Figure 2), for the training data.
Figure 2. Ensemble building with the same model type
Modern ensemble techniques rely on more than bagging to generate variability in their base learners. For instance, random forests, an ensemble of decision trees, employ bagging as well as a random selection of candidate input features at each tree split to increase variation in base learners. Even though the structure of individual trees can be quite variable— with different features selected in splits, different parameter values, and variation in the location and depth of splits in the trees—the underlying structure of the model never changes. We’re restricted to the same structural entities – decision trees in this example, without knowing if trees are the best method to solve our problem. By depending on a single model type in our ensemble, we risk building many weak base learners with common limitations while misclassifying the same cases, or subsets of cases, with similar properties. Boosting is a technique that can overcome these shortcomings. With boosting, models are built in sequence, and later ones correct the errors of earlier ones by upweighting errors. That is, new models pay more attention to the training cases misclassified previously.
Decision trees are the most popular base models of ensemble learning. R, Python and standard statistical software incorporate off-the-shelf commands to implement ensemble methods in trees. However, ensemble methods can be used to combine predictions from all types of predictive models. One drawback is that custom code may be required to build the bundled model ensemble and to perform the necessary accounting. This involves using the same data for training and for out-of-sample evaluation, and for generating the overall ensemble score or class for each case via averaging, voting, or some other method.
Netflix Competition
Ensembles played a major role in the 2006 million-dollar Netflix contest. At the time, Netflix wanted to improve the “Cinemax” model they used to recommend movies for users (this was in the DVD era, before Netflix became a major content producer itself). They decided to share a large amount of customer rating data with the public in hopes of crowdsourcing a better model, offering a million dollar prize for a model that produced a 10% improvement over Cinemax (measured by RMSE – root mean squared error).
Analysts competing in the contest quickly achieved about an 8% improvement with their individual models, and then progress slowed. At that point, individuals began coalescing into groups to combine their models into ensembles, which yielded incremental improvement.* Then groups joined together into larger groups, yielding further (smaller) improvement. Finally, the “BellKor” and “Big Chaos” teams joined together into “BellKor’s Pragmatic Chaos,” topped 10% and claimed the prize, just 20 minutes before an even larger super-team also crested the 10% threshold.
Conclusions and Caveats
Ensembles have been one of the most successful developments in predictive modeling, generating predictions that consistently outperform individual models. Consistently does not mean “always” – in a given situation, there may exist a top-performing model that outperforms the ensemble. But the track record of ensembles sets a high bar for choosing an individual model over the ensemble.
The Netflix Prize contest revealed another important caveat – practicality. Though the conceptual steps to combine multiple predictions may seem trivial, the development of too many constituent individual models and the coding effort to implement and then combine them can outweigh the benefit. Recall that 80% of the improvement in the Netflix contest was achieved quickly with algorithms that were, in retrospect, minimalist. In the real world business context, significant improvement with parsimonious models often trumps the incremental gain that comes only with much greater effort. A quick, simple and good model not only eases deployment, but also facilitates the intra-organizational communication needed to assure that the right question is being answered.
In the event, Netflix ended up not using the full BellKor Pragmatic Chaos model, saying the engineering effort required was too great. Not only was the winning model complex, but Netflix’s business shift from DVD’s to streaming, and from households to individuals, complicated the recommendation task. It did, however, end up using a simpler ensemble, the prize winner from an earlier round, that yielded 8.43% improvement. Even in ensembles, parsimony is a virtue.
P.S. Back to the ox… Galton, a committed eugenicist and advocate of elite rule, was sufficiently surprised by the “wisdom of the crowd” that he tempered his elitist views and conceded, in a 1907 article in Nature, that there might be some merit in the “vox populi” (as he titled his article).
*Interest in ensembles amongst Netflix competitors got its first boost when the team “Ensemble Experts” (Woodriff, Elder, Vogel) suddenly appeared in second place on the leaderboard, when there were 10,000 contest entrants.